宇宙に始まりはなく、過去が無限に続いている?

量子力学理論の１つである因果集合理論

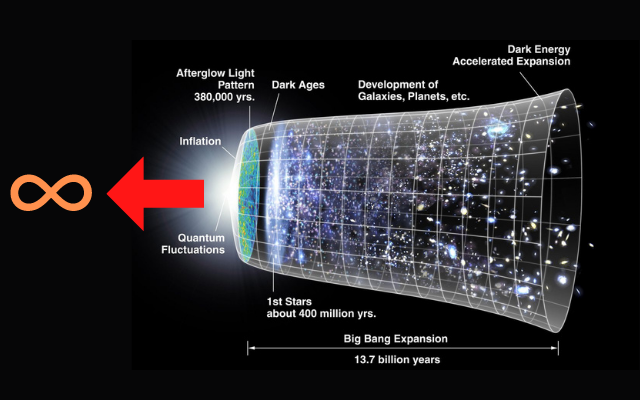
宇宙にある銀河は地球からの距離に比例したスピードで遠ざかっている観測事実から、宇宙は膨張していると考えられている。

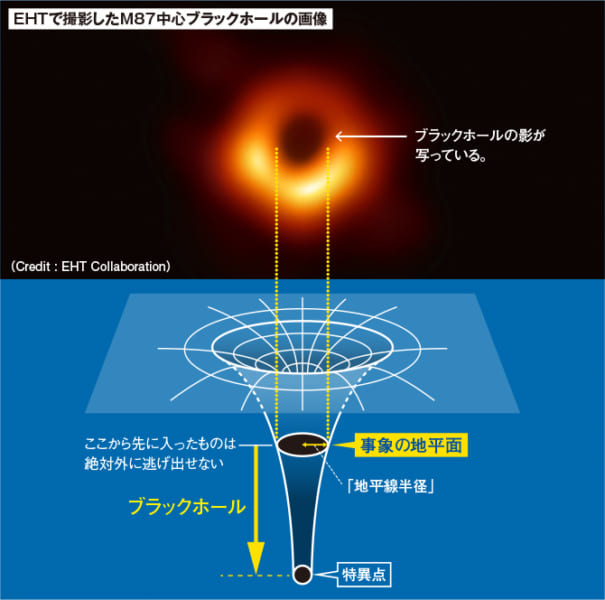
この膨張の逆をたどれば、ゼロという特異点を推定できるが、ゼロなので物理理論は適用できない。

特異点では重力は無限大になるので、それよりも過去は存在できないので、宇宙は特異点からはじまったとすることになっていた。

ビッグバン宇宙論では特異点を避けることができないことが、特異点定理から導き出され、特異点では理論が使えないので神の領域とすることなるので、特異点を避ける宇宙モデルの構築に物理学者は取り組んでいた。

相対性理論ではミクロの宇宙を記述することができないので、登場したのが「量子重力理論」である。

具体例としては「超ひも理論」などだが、どれも完成には至っていない。

量子力学ではエネルギーがとる値は連続的なものではなく、飛び飛びの不連続なもの、すなわち「離散的」であるように、因果集合理論では、連続的だと思われていた時空も実は不連続になっている前提からはじまる。

量子力学では超ひもなどの最小単位があるように、因果集合理論では時空にも最小単位があることを前提とすることで、膨張している宇宙の時間を過去に遡っていっても宇宙の大きさは有限にとどまりゼロにならないので、ビッグバンより過去も計算可能になる。

因果集合理論では、時空を原因と結果の因果関係で結ばれた出来事の集合と考え、この因果関係の連鎖から時間の流れが生まれるとする。

そこで因果関係に始まりが本当に必要なのかどうかを調べた結果、因果集合は過去に向かって無限に続く可能性があることが分かった。

ある事象の前には常に原因となる事象がある状態となり、ビッグバンという宇宙の始まりは必要とされない。

ビッグバンは変化の途中にある１つの通過点に過ぎず、そこを起点にする理由が一つもない。

The Universe May Have Never Begun, Physicists Say　

時間と空間の起源

論文　time had no beginning　https://arxiv.org/abs/2109.11953

宇宙はビッグバンによって始まり、それ以前は「無」だったというのが現在の定説となっています。

けれど、もしかしたら私たちの宇宙は常に存在していて始まりはなかった可能性が、新たな量子重力理論によって示されました。

イギリス・リバプール大学(University of Liverpool)の研究チームは、因果集合理論（causal set theory）と呼ばれる量子重力の新しい理論を使い、宇宙の始まりについて計算したところ、宇宙に始まりはなく無限の過去に常に存在していたという結果を得ました。

この結果に従うと、ビッグバンは宇宙が遂げた最近の進化の1つでしかないということになります。

この研究成果は、9月24日にプレプリントサーバー『arXiv』で公開された論文に掲載されています。

· 物理学が未だに説明できていない問題

· 時間と空間とはなんなのか？

· ビッグバンは通過点に過ぎない

物理学が未だに説明できていない問題

現在、物理学にはまったく異なる2つの理論が存在し、どちらも大きな成功を収めています。

その2つの理論とは、量子力学と一般相対性理論です。

量子力学は、自然界を支配する4つの基本的な力のうち、3つの力（電磁気力、弱い力、強い力）を微小な世界で記述することに成功しました。

ただ、重力についてはまだうまく説明することができていません。

一方、一般相対性理論は、これまで考案された中でもっとも強力で完全な重力の記述方法です。

しかし、一般相対性理論にも不完全な部分があり、この世界で2つのポイントについてだけ理論が破綻しています。

それが「ブラックホールの中心」と「宇宙の始まり」です。

ここについては、一般相対性理論でも計算が破綻してしまい、信頼できる結果を得ることができません。

そのため、これらの領域は「特異点」と呼ばれていて、現状の物理理論が及ばない時空のスポットとされています。

これは、一般相対性理論が数学的につまづいているポイントでもあります。

ブラックホールの質量は時空の曲率が無限大になる特異点に集中している / Credit:京都産業大学,Catch Up WORLD

この2つの特異点で、一般相対性理論がうまく機能しない理由は、この場所では重力が非常に小さなスケールで非常に強くなっているためです。

一般相対性理論はマクロな世界を記述する古典物理学の理論のため、微視的な世界の重力をうまく取り扱うことはできていません。

一般相対性理論は重力を時空の曲率として表現しています。

投げたボールが地面に落ちるのは、地球が歪めた空間に沿って、ボールが軌跡を曲げ、それが地面と交わるためです。

しかしあまりに微視的な世界では、空間が歪むだけでは重力を記述できません。アインシュタインも生涯この問題に悩んでいました。

そのため、この微視的な世界の強い重力を記述するための新しい理論が必要となります。

そこで、現在考えられているのが「量子重力理論」です。

ただこの理論も「超ひも理論」や「ループ量子重力」など、さまざまな候補が存在していますが、まだ完成されていません。

しかし、そのすべてが同じような方向から問題のアプローチをかけています。

それが「時間と空間というものがなぜ存在するのか？」「どこから生じているのか？」「そもそも時空のもっとも基本的な構造とはなんなのか？」ということです。

量子重力理論を考えたとき、いずれの候補理論も、時間と空間がもっと根本的な何かから生じているということを考慮しないとうまく話が進まないのです。

そして、この疑問に対処する、新しいアプローチが登場しています。

それが「因果集合理論」です。

時間と空間とはなんなのか？

今回の研究チームの一人、英国リバプール大学の物理学者ブルーノ・ベントー氏は時間の本質について研究を行っています。

彼は宇宙の始まりを考えるという今回の研究において、「因果集合理論」と呼ばれるものを採用しました。

あまり聞き馴染みのない理論ですが、「因果集合理論」とはどのような理論でしょうか？

現在の物理学では、時間や空間はなめらかに連続した布のようなものとして捉えられています。

こうした連続した時空では、2つの点は空間的に可能な限り近くに存在し、2つの事象は時間的に可能な限り近くで発生します。

しかし、「因果集合理論」では空間と時間をなめらかな連続につながったものとは考えていません。

この理論では、時空を極限まで分解していくと原子のような離散的（飛び飛びの値で変化する）な塊になると解釈しています。

つまり、時空には最小の基本単位が存在するというのです。

映像が小さな画素の集合であるように、時空間も最小単位が因果で結ばれた集合かもしれない / Credit:canva

今この記事を読んでいる画面も、なめらかな一枚の画像に見えるでしょうが、当然虫眼鏡などで拡大すれば、それは小さな1ピクセルの画素が並んでいるものだとわかります。

空間も同様に分割されていて、その最小単位以上にはお互い近づくことができないかもしれないというのです。

この考え方の何が重要なのかというと、この理論に従った場合、ビッグバンやブラックホールのような特異点の問題がきれいに取り除くことができるからです。

なぜなら、この理論では時空を無限に小さく圧縮することが不可能だからです。

時空には最小単位の「時空の原子」があり、その大きさを超えて小さくなることはありえないため、特異点が存在しなくなるのです。

では、ビッグバンに特異点がない場合、宇宙の始まりはどのようなものになるのでしょうか？

ビッグバンは通過点に過ぎない

ベントー氏は、因果集合理論が宇宙の最初の瞬間をどのように表現するか、インペリアル・カレッジ・ロンドンのスタブ・ザレル氏と共同で研究を勧めました。

従来の因果集合理論では、因果集合は無から生じて現在の宇宙まで成長したとされています。

しかし、彼らは、そもそも因果集合に始まりが必要かどうかということを検討しました。

すると、彼らの研究では、因果集合は過去に向かって無限に続き、常に前に何かがある状態となり、ビッグバンという始まりは存在しないことがわかったのです。

彼らの理論によれば、私たちがビッグバンと認識しているものは、この常に存在する因果集合の進化における特定の瞬間に過ぎず、真の始まりではなかった可能性があるとのこと。

ビッグバンは進化の通過点に過ぎず、宇宙の過去は無限に続いている可能性がある / Credit:NASA
,
ただ、この理論はまだ少数の物理学者が注目する理論でしかなく、論文も査読付き科学雑誌への掲載はまだ決まっていません。

宇宙の過去が無限にあるということが、物理的に何を意味しているのかも、まだよくわかりません。

とはいえ、宇宙に始まりがないということは、**少なくとも数学的には可能**なことなのです。

因果集合 (causal sets) プログラムは量子重力へのアプローチの一つである。これは、時空は本質的に離散的であり時空の事象はすべて半順序によって関連しているという仮定に基づいている。この半順序は時空の事象間の因果関係という物理的意味を持っている。

概要

このプログラムはDavid Malamentによる定理[1]に基づいている。この定理は、もしそれらの因果構造を保存する二つの過去と未来が区別可能な時空の間の全単射写像があるならば、その写像は等角同型であることを述べている。未定の共形因子は時空における体積と関係する。この体積因子は時空の各点の体積要素を規定することにより、正しい値を推定することができる。そのとき、時空領域の体積はその領域内の点の数を数えることにより見出すことができるであろう。

因果集合はRafael Sorkinによって創始された。彼はこのプログラムの主要な推進者であり続けている。彼は上述の議論を特徴付けるために、"順序 + 数 = 幾何"というスローガンを作った。このプログラムは、時空は局所ローレンツ不変性を保つ一方で根本的に離散的であるような理論を与える。

定義

因果集合 (causal set または causet) は、半順序関係 $\preceq$ {\displaystyle \preceq } $⪯$ $を持つ集合$ {\displaystyle C} $C$ $、$ すなわち · 反射：すべての{\displaystyle x\in C}x∈Cx∈Cについて、{\displaystyle x\preceq x}x⪯xx⪯xが成立する。 · 反対称：すべての{\displaystyle x,y\in C}x,y∈Cx,y∈Cについて、x⪯y⪯x⟹x=yx⪯y⪯x⟹x=yが成立する。 · 推移関係：すべての{\displaystyle x,y,z\in C}x,y,z∈Cx,y,z∈Cについて、{\displaystyle x\preceq y\preceq z}x⪯y⪯zx⪯y⪯zならば{\displaystyle x\preceq z}x⪯zx⪯zが成立する。 · 局所有限：すべての{\displaystyle x,z\in C}x,z∈Cx,z∈Cについて、**card**({y∈C|x⪯y⪯z})<∞({y∈C|x⪯y⪯z})<∞が成立する。ここで、**card**({\displaystyle A}A) は集合{\displaystyle A}Aの濃度 (cardinality) を表す。以後、{\displaystyle x\preceq y}x⪯yx⪯y かつ {\displaystyle x\neq y}x≠yx≠yならば、{\displaystyle x\prec y}x≺yx≺yと書く。集合{\displaystyle C} $C$ $は時空の$ 事象の集合を表し、順序関係 $\preceq$ {\displaystyle \preceq } $⪯$ $は事象間の因果関係を表す。$

（ローレンツ多様体における類似の概念については因果構造も参照のこと。）

この定義は反射的な順序関係の慣習に基づくが、非反射的な順序関係の慣習を選ぶこともできる。（閉じた因果曲線のない）ローレンツ多様体の因果関係は最初の三つの条件を満たす。局所有限条件は時空の離散性を導く。

**連続体との比較**

ある因果集合が与えられたとき、それをローレンツ多様体に埋め込むことができるであろうか。埋め込みとは、因果集合の要素を因果集合の順序関係が多様体の因果順序に適合するように多様体の中に入れる写像である。しかしながら、埋め込みが適切である前にさらなる基準が求められる。もし、平均として、多様体のある領域に写像される因果集合要素の数がその領域の体積と比例するなら、その埋め込みは忠実である (faithful) と言われる。この場合、その因果集合は'多様体様 (manifold-like) 'であると見なすことができる。

因果集合プログラムへの中心的な予想は、同じ因果集合は大きなスケールで類似していない二つの時空へ忠実に埋め込むことはできないというものである。これは'基本予想' (fundamental conjecture) を意味する hauptvermutung と呼ばれる。二つの時空が'大きなスケールで類似する'ときを決定するのが困難なため、この予想を厳密に定義することは困難である。

時空を因果集合としてモデル化することは、われわれの関心をこのような'多様体様'の因果集合に制限することを要求するだろう。

**まき散らし**

1+1次元内の1000個のまき散らされた点のプロット

ある因果集合をある多様体に埋め込むことができるかどうかを決定することの困難には逆方向からアプローチすることができる。ローレンツ多様体上へまき散らした点によって因果集合を作ることができる。その時空領域の体積に比例する数の点をまき散らし、それらの点の間の順序関係を誘導するために多様体上の因果順序関係を用いることによって、（構成によって）その多様体に忠実に埋め込むことのできる因果集合を生成することができる。

ローレンツ不変性を保つために、これらの点はポアソン過程を用いてランダムにまき散らされなければならない。

このように、{\displaystyle n}n個の点を体積{\displaystyle V}Vの領域上まき散らす確率は

である。

ここで、ρはまき散らしの密度である。

ある正則格子上への点のまき散らしでは、点の数とその領域の体積の比例関係は保たれないであろう。

**幾何学**

多様体におけるいくつかの幾何的な構成を因果集合に適用することができる。これらを定義したとき、因果集合が埋め込まれる可能性のある背景のどの時空にも基礎をおくのではなく、因果集合自身のみに基礎をおくことに注意が必要である。これらの構成の概要は脚注を参照のこと[2]。

**測地線**

ある因果集合内の*リンク* *(link)* とは、{\displaystyle x\prec y}x≺yx≺yとなる一対の要素{\displaystyle x,y\in C\,\!}x,y∈Cx,y∈Cで、{\displaystyle x\prec z\prec y}x≺z≺yx≺z≺yとなる{\displaystyle z\in C\,\!}z∈Cz∈Cは持たない。

チェーン (chain) とは、{\displaystyle i=0,\ldots ,n-1}i=0,…,n−1i=0,…,n−1について{\displaystyle x_{i}\prec x_{i+1}}xi≺xi+1xi≺xi+1となる要素の列x0,x1,…,xnx0,x1,…,xnである。チェーンの長さ{\displaystyle n}nnは使われた関係の数である。

これは二つの因果集合要素の間の測地線を定義するために用いることができる。二つの要素{\displaystyle x,y\in C}x,y∈Cx,y∈C間の測地線は次の条件を持つリンクのみで構成されたチェーンである：

2. チェーンの長さ{\displaystyle n}nは{\displaystyle x\,}xから{\displaystyle y\,}yへのチェーン全体にわたる最大.

一般的には、二つの要素の間に一つ以上の測地線が存在する。

Myrheim[3]は、そのような測地線の長さは二つの時空点を結ぶある時間的測地線に沿った固有時に直接比例するべきであることを最初に示唆した。平坦な時空にまき散らされて生成された因果集合を用いて、この予想の検証がなされている。この比例関係が成立することは示され続けてきており、曲がった時空にまき散らされた因果集合でも同様に成り立つことが予想されている。

**次元推定**

ある因果集合の多様体次元を推定するための多くの研究がなされている。これには、忠実に埋め込むことのできる多様体の次元を与えることを目的としている因果構造を用いるアルゴリズムを含む。このアルゴリズムは今までのところ、因果集合を忠実に埋め込むことのできるミンコフスキー時空の次元を見つけることに基づいて開発されている。

Myrheim-Meyer次元

このアプローチは、{\displaystyle d}d-次元ミンコフスキー時空にまき散らされた因果構造内に存在する{\displaystyle k}k-長のチェーンの数の推定に基づいている。次に、因果構造内の{\displaystyle k}k-長のチェーンの数を数えることで、{\displaystyle d}dについて推定することができる。

中点スケーリング次元

このアプローチは、ミンコフスキー時空内の二点間の固有時とその二点間の時空間隔の体積との関係に基づいている。（固有時を推定するために）二点{\displaystyle x\,}xと{\displaystyle y\,}yの間の最大チェーン長を計算し、（時空間隔の体積を推定するために）{\displaystyle x\prec z\prec y}x≺z≺yとなる要素{\displaystyle z\,}zの数を数えることで、時空の次元を計算することができる。

これらの推定方法は{\displaystyle d}d-次元ミンコフスキー空間へ高密度でまき散らされることで生成された因果集合の正しい次元を与えるべきである。共形平坦な時空における検証[4]は、これら二つの方法が正確であることを示している。

動力学

因果集合の正しい動力学を開発する課題が進行中である。これらは、どの因果集合が物理的に現実的な時空に一致するかを決定する規則の集合を与えるであろう。因果集合動力学を開発する最も有名なアプローチは量子力学の歴史の和 (sum-over-histories) による立場に基づいている。このアプローチは、因果集合の一要素を同時に成長 (growing) させることによって"因果集合の和 (sum-over-causal sets) "を実行しうる。各要素は量子力学の規則に従って足し合わされ、干渉は大きな多様体様の時空がその貢献に最も重要であることを確かにするであろう。当面のところ最も良い動力学モデルは各要素が確率に従って足し合わせられる古典モデルである。このモデルはDavid Rideoutとen:Rafael Sorkinによるもので、古典逐次成長力学 (classical sequential growth : CSG) 動力学として知られている[5]。古典逐次成長力学モデルは新しい要素を次々と足し合わせていくことで因果集合を生成する方法である。新しい要素をどのように足し合わせていくかの規則が規定されており、モデルのパラメータに依存して異なる因果集合を生じる。